tags: leetcode easy Tree Depth-First Search Binary Search Tree Binary Tree

938. Range Sum of BST

Description

Given the root node of a binary search tree and two integers low and high, return the sum of values of all nodes with a value in the inclusive range [low, high].

Examples

Example 1:

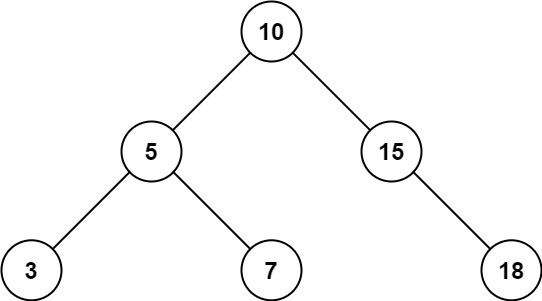Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2:

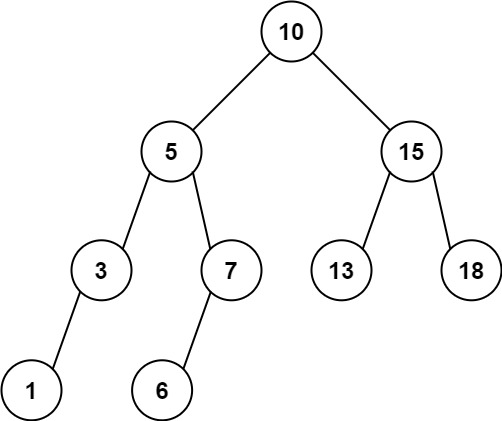Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Constraints:

• The number of nodes in the tree is in the range [1, 2 * 104].
• $1 \leq Node.val \leq 10^5$
• $1 \leq low \leq high \leq 10^5$
• All Node.val are unique.

Code

• Type 1

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int rangeSumBST(struct TreeNode* root, int low, int high) {
    if (!root)
        return 0;
    return (((root->val >= low) && (root->val <= high)) ? root->val : 0) +
           ((root->right) ? rangeSumBST(root->right, low, high) : 0) +
           ((root->left) ? rangeSumBST(root->left, low, high) : 0);
}

• Type 2

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int rangeSumBST(struct TreeNode* root, int low, int high) {
    if (!root)
        return 0;
    if (root->right) {
        if (root->left) {
            return (((root->val >= low) && (root->val <= high)) ? root->val : 0) +
                rangeSumBST(root->right, low, high) +
                rangeSumBST(root->left, low, high);
        }
        return (((root->val >= low) && (root->val <= high)) ? root->val : 0) +
            rangeSumBST(root->right, low, high);
    }
    if (root->left) {
        return (((root->val >= low) && (root->val <= high)) ? root->val : 0) +
            rangeSumBST(root->left, low, high);
    }
    return (((root->val >= low) && (root->val <= high)) ? root->val : 0);
}

• Type 3

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int rangeSumBST(struct TreeNode* root, int low, int high){
    if(!root) return 0;
    int result = 0;
    result += ((root->val >= low) && (root->val <= high)) ? root->val : 0;
    if(root->left) result += rangeSumBST(root->left, low, high);
    if(root->right) result += rangeSumBST(root->right, low, high);
    return result;
}

Complexity

Space	Time
$O(1)$	$O(N)$

Result

• Type 1 :
  • Runtime : 94 ms, 89.94%
  • Memory : 42.4 MB, 43.58%
• Type 2 :
  • Runtime : 93 ms, 92.74%
  • Memory : 42.5 MB, 21.23%
• Type 3 :
  • Runtime : 91 ms, 94.41%
  • Memory : 42.4 MB, 58.66%